EfficientNet 논문 리뷰

EfficientNet : Rethinking Model Scaling for Convolutional Neural Networks [paper]
저자 : Mingxing Tan, Quoc V. Le

Summary

• Proposed ‘Compound Scaling Method’, which can scale ConvNet by efficiently balancing network Depth, Width, Image Resolution
• Proposed ‘EfficientNet’, which achieved SOTA accuracy with much more efficient model size and complexity

Problems to solve

• In previous work, it was common to scale only one of the three dimensions : depth, width, and image resolution
  • Depth : The number of ConvNet layers
  • Width : The number of channels of each ConvNet layer
  • Image Resolution : Input image size (Height*Width)
• Is there a principled method to scale up ConvNets that can achieve better accuracy and efficiency?

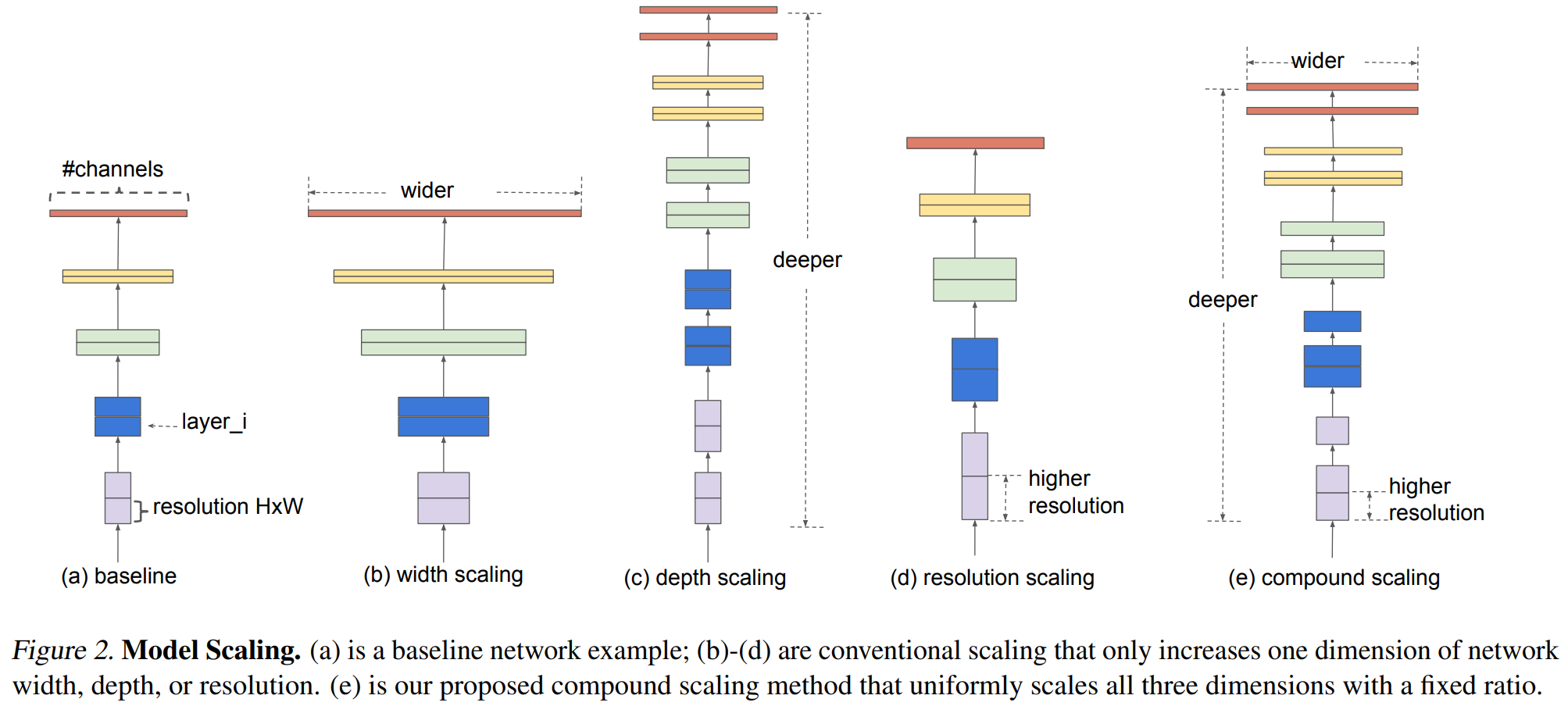
Compound Scaling Method

Problem Formulation

• Define ConvNet Layer $i$ as $Y_i = \mathcal{F_i}(X_i)$
  • where $Y_i$ : Output Tensor, $\mathcal{F_i}$ : Operator, $X_i$ : Input Tensor
  • $X_i$ is a tensor with shape of $(H_i, W_i, C_i)$, where $H_i, W_i, C_i$ is height, width, channel of the tensor, respectively
• A list of ConvNet layers is represented as 

\[\mathcal{F_k}\odot ... \odot \mathcal{F_2} \odot \mathcal{F_1} = \bigodot _{j=1,...,k}\mathcal{F_j}(X_1)\]

• Let’s consider a list of ConvNet layers as block, then ConvNet $N$ can be defined as

\[\mathcal{N}=\bigodot _{i=1,...,s}\mathcal{F_i}^{L_i}(X_{<H_i,W_i,C_i>})\]

• where $\mathcal{F_i}^{L_i}$ is $\mathcal{F_i}$ repeated $L_i$ times in stage $i$

• Then, the target is to maximize the model accuracy for any given resource constraint
• In order to reduce the search space…
  • No architecture($\mathcal{F_i}$) changing
  • All layers must be scaled uniformly with constant ratio

\[max_{d,w,r} (Accuracy(\mathcal{N}(d,w,r)))\] \[s.t.\quad \mathcal{N}(d,w,r) = \bigodot _{i=1,...,s}\hat {\mathcal{F_i}}^{d \cdot \hat L_i}(X_{<r\cdot \hat H_i,r\cdot \hat W_i,w\cdot \hat C_i>})\] \[\mathsf{Memory}(\mathcal{N}) \le \mathsf{TargetMemory} \quad \quad\] \[\mathsf{FLOPS}(\mathcal{N}) \le \mathsf{TargetFlops} \quad \quad \quad\]

Scaling Dimensions

• Deeper : Captures richer and more complex features
• Wider : Captures more fine-grained features and easier to train
• Higher Resolution : Captures more fine-grained patterns

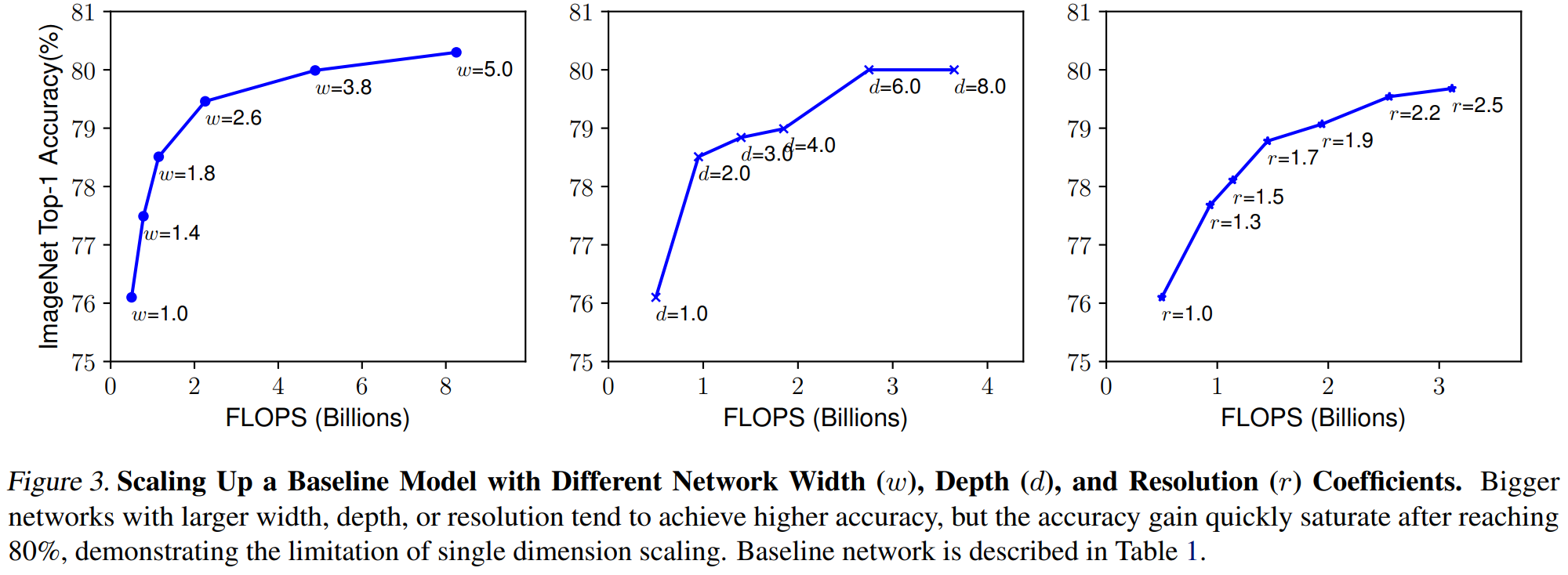
• Scaling up any dimension of network improves accuracy, but the accuracy gain diminishes for bigger models

Compound Scaling

• Intuitively, higher resolution images deeper and wider network
• To validate this intuition, they scaled network width w by fixing d and r

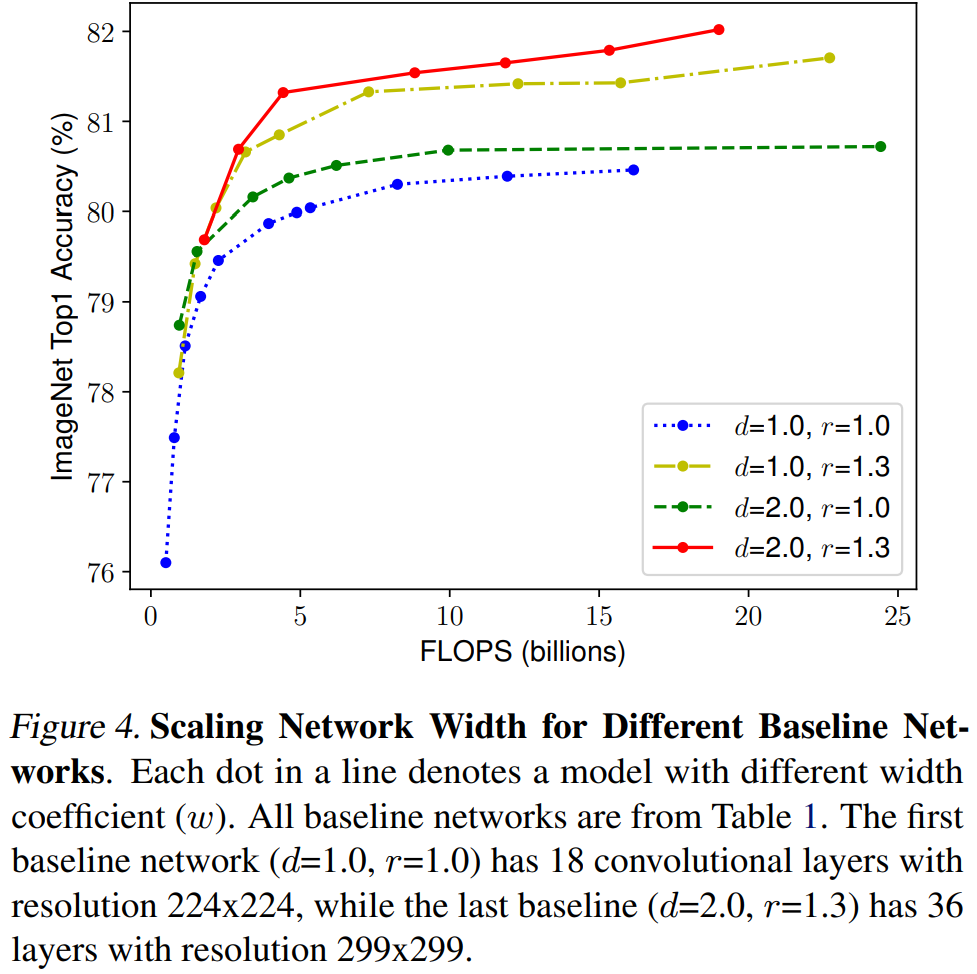
• For better accuracy and efficiency, it is critical to balance the network width, depth, and resolution

Compound Scaling Method

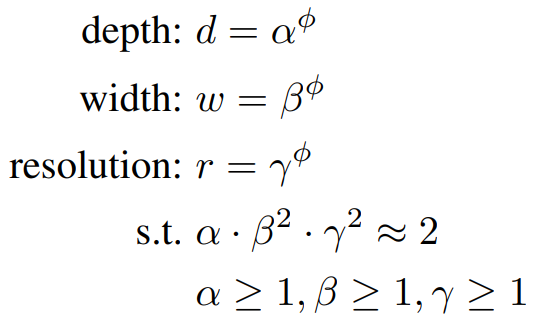
• $\alpha, \beta, \gamma$ : constants to adjust the network depth, width, image resolution, respectively. These components are determined by a small grid search
• $\phi$ : variable to decide how many resources to use for model scaling
• FLOPS of ConvNet $\propto d, w^2, r^2 $
• FLOPS of ConvNet $\propto (\alpha \cdot \beta^2 \cdot \gamma^2 )^\phi$
• Set $\alpha \cdot \beta^2 \cdot \gamma^2 \approx 2$, so that the total FLOPS will increas approximately by $2^\phi$
• Once $\alpha, \beta, \gamma$ are decided, the model scaling can be easily done only by adjusting $\phi$

EfficientNet Architecture

• Compound Scaling Method does not change layer operators $\hat {\mathcal{F_i}}$ in baseline network but having a good baseline network is also critical
• By NAS(Neural Architecture Search) to optimize accuracy and FLOPS, an accurate and efficient baseline is proposed
• Optimization goal : $ACC(m) \times [FLOPS(m)/T]^w$
  • $ACC(m)$ : Accuracy of model $m$
  • $FLOPS(m)$ : FLOPS of model $m$
  • $T$ : Target FLOPS (Here, $T$ = 400 million)
  • $w$ : hyperparameter for trade-off (Here, $w=-0.07$)