Boxplot에 대해 알아보자
Boxplot이란 다음과 같은 그래프를 말한다.
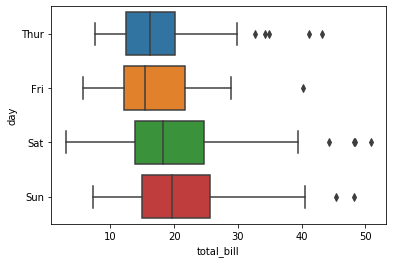
이번 포스트에서는 이 Boxplot에 대해서 알아보겠다.
Boxplot이란?
위의 Boxplot 샘플을 보면 무슨 선도 있고 점도 있고 박스도 있어서 복잡해보이는데, 그만큼 많은 정보를 담고 있어 데이터의 분포를 표현하는 데에 적합한 그래프이다. 어떠한 정보를 담고 있는지 다음의 그림에서 보자.
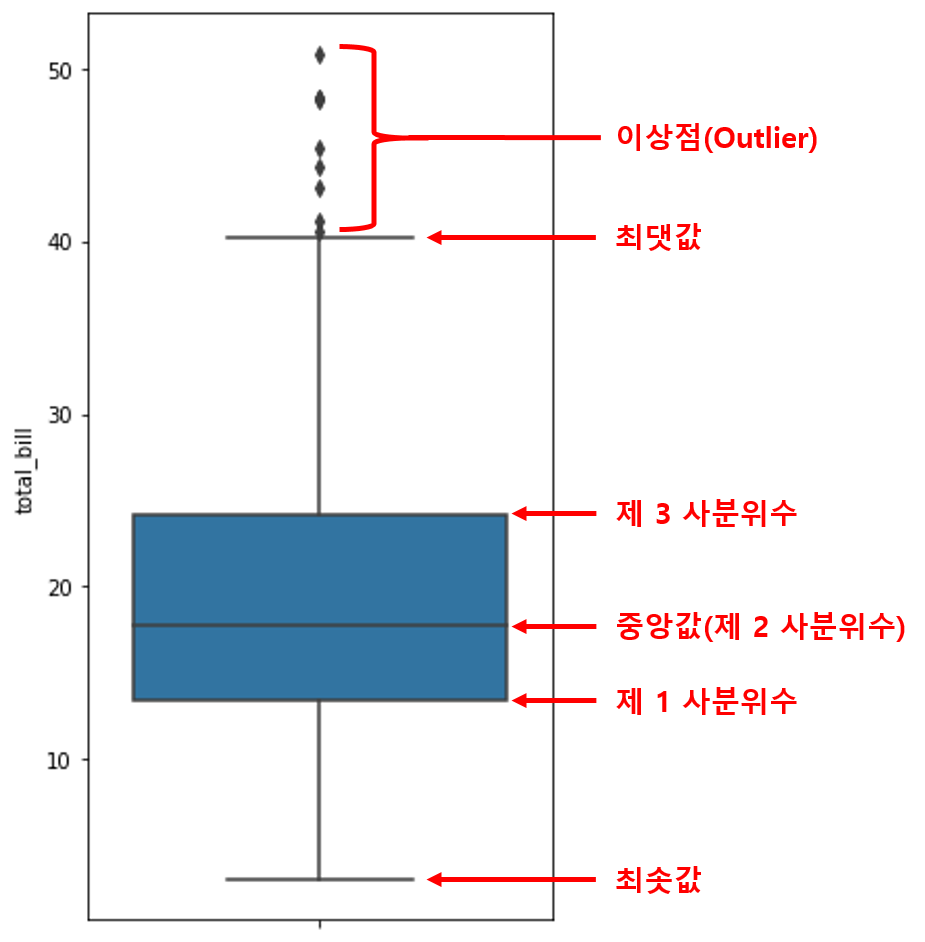
하나하나 쉬운 용어부터 설명하겠다.
중앙값
중앙값(Median)말 그대로 데이터를 크기 순으로 일렬로 나열했을 때 중앙에 위치한 값이다. 평균과는 다른데, 다음의 분포를 예시를 들며 설명하겠다.
[1,2,3,4,5,6,7,8,9,10]
1부터 10까지의 정수가 있는 분포를 생각해보자. 이 분포의 평균은 5.5이며, 이 분포의 중앙에 위치한 값, 즉 중앙값은 5와 6의 사이인 5.5가 된다.
그러면 두 번째 분포를 생각해보자.
[1,2,3,4,5,6,7,8,9,1000]
위의 예시에서 10을 1000으로 바꾸었다. 숫자 하나 바뀌었을 뿐인데 이 분포의 평균은 갑자기 뛰어서 104.5가 된다.
반면 중앙값은? 똑같이 5.5이다.
1000과 같이 다른 데이터와 확연히 다른 데이터를 이상점(Outlier)이라고 한다. 혹은 이상치, 특이점이라고도 한다.
평균은 이러한 이상점에 대해 많은 영향을 받으며, 중앙값은 이상점의 영향으로부터 비교적 자유롭다.
이를 다른 말로 하면 평균은 이상점에 대해 민감하며(Sensitive), 중앙값은 이상점에 대해 강건하다(Robust)고 할 수 있다.
어쨌든 중요한 것은, 이상치가 있는 분포에서는 평균보다 중앙값이 대푯값에 더 알맞다는 말이다. 따라서 Boxplot에서는 평균이 아닌 중앙값을 표시한다.
제 1, 3 사분위수
위에서 설명한 중앙값은 다른 말로 하면 분포의 상위/하위 50%에 위치한 수라고 할 수 있다. 그렇다면 하위 25%에 위치한 수와 상위 25%에 위치한 수 또한 구할 수 있을 것이다.
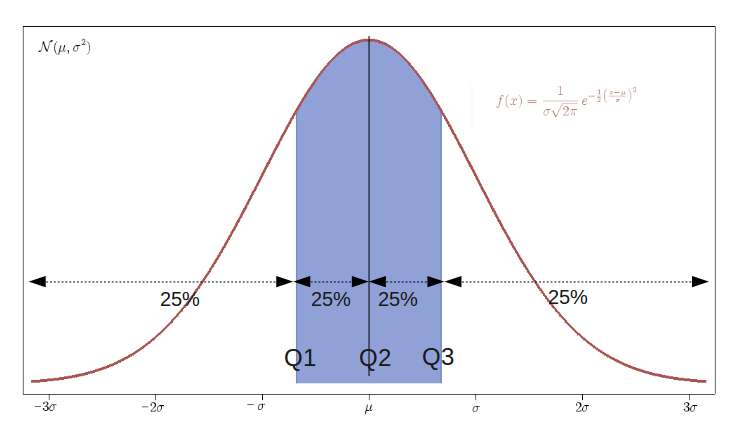
(그림 출처 : Wikipedia)
위의 그림처럼 일반적인 Gaussian Distribution 등을 생각해보면 하위 25%에서 상위 25%까지의 범위는 매우 좁지만 전체 데이터의 반을 차지하고 있어 매우 의미있는 수라고 할 수 있다. 또한 중앙값과 마찬가지로 이상점에 대해 강건하다는 장점도 있다.
데이터의 전체 갯수를 4등분 했을 때 나오는 세 수를 각각 하위 25%에 해당하는 제 1 사분위수(1st Quartile, Q1), 하위/상위 50%에 해당하는 제 2 사분위수(2nd Quartile, Q2) 혹은 중앙값, 그리고 상위 25%에 해당하는 제 3 사분위수(3rd Quartile, Q3)라고 부른다.
이 1, 3 사분위수는 Boxplot에서 상자의 양 변으로 표현된다. 이 때 상자의 양 변 간의 거리, 즉 제 1 사분위수와 제 3 사분위수 사이의 거리를 사분범위(Interquartile range, IQR)라고 한다.
최댓값, 최솟값, 이상점
위의 Boxplot의 예시를 보면 한 가지 이상한 점을 발견할 수 있다. 분명 최댓값이라고 적혀있는데 그 위에 점으로 표시된 데이터가 더 있지 않은가? 이 점으로 표시된 데이터가 바로 위에서 언급한 이상점이다. 같은 분포 내의 다른 데이터와는 확연히 다른 양상을 보이는 데이터이기 때문에 이러한 이상점은 따로 분리를 해주는 것이 일반적이며, 이상점을 분리하고 난 후에 최댓값과 최솟값을 구한다. 이 최댓값과 최솟값은 박스에서 이어져 나온 선분으로 표시되며, 수염(Whisker)라고도 불린다.
그러면 이 이상점을 어떻게 분리를 할 수 있을까? 위에서 언급한 사분범위(IQR)가 사용된다. 이 제 1사분위수보다 IQR*1.5 이상으로 작은 값과, 제 3 사분위수보다 IQR*1.5 이상으로 큰 값이 이상점으로 취급된다. 그리고 저 범위를 Inner Fence라고 한다. 이 Inner Fence 내에서의 최댓값과 최솟값이 데이터 분포 전체에서의 최댓값과 최솟값으로 표현되는 것이다.
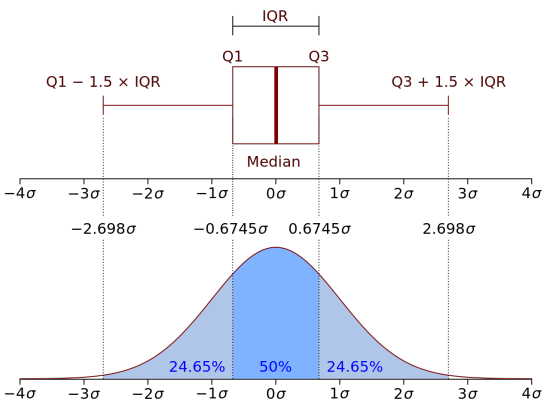
(그림 출처 : Wikipedia)
Seaborn을 이용한 Boxplot
Seaborn을 통해서 Boxplot을 매우 쉽게 그릴 수 있다. 데이터를 우선 DataFrame으로 만들고 나면 x축, y축, hue를 정하는 것만으로도 간단하게 Boxplot을 그려준다.
이에 대한 예시로는 Seaborn Documentation에 잘 설명되어 있으니 참고하자.
Violin Plot
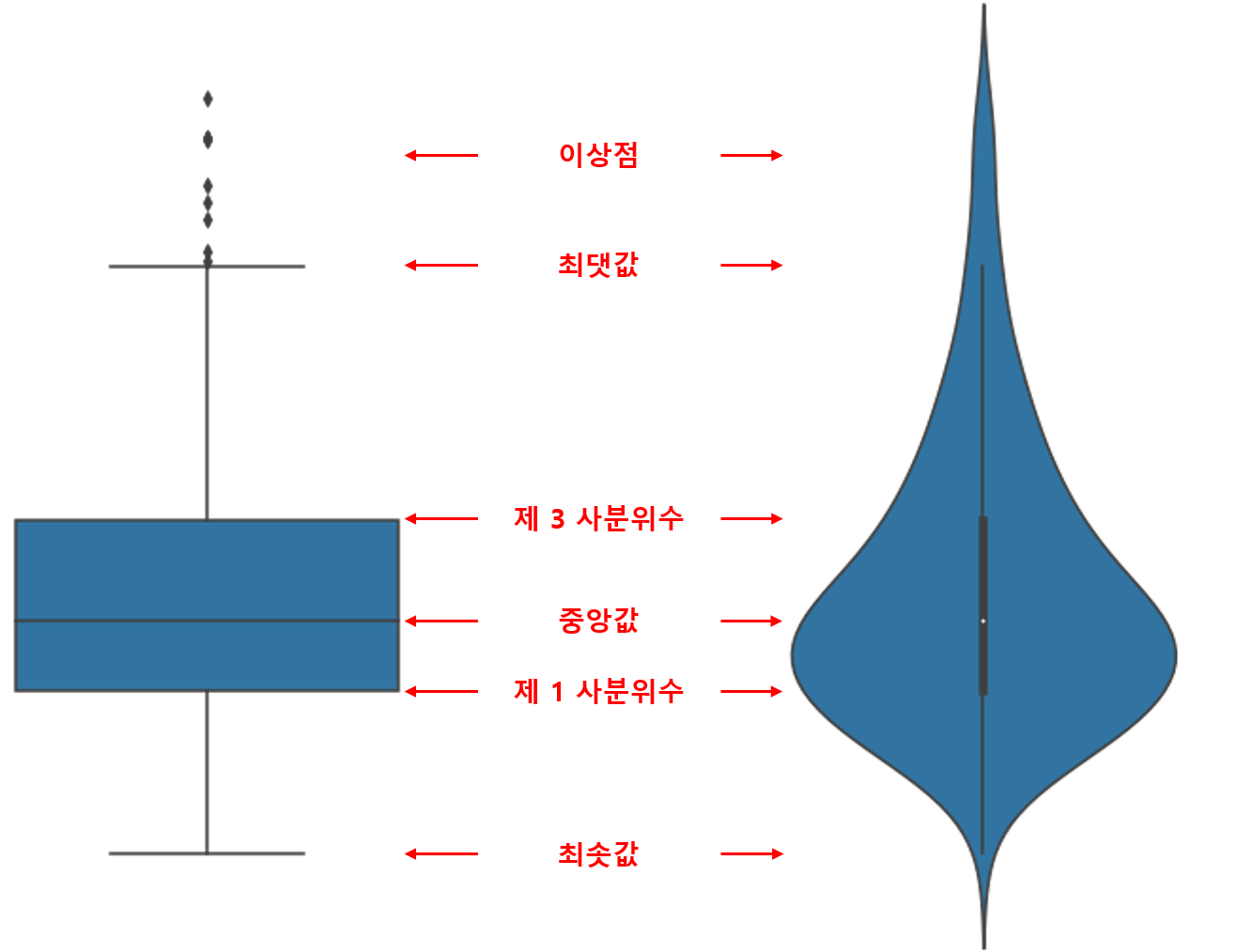
자매품(?)으로 Violin Plot이라는 것이 있다.
BoxPlot이 담고 있는 모든 정보를 제공하며, box 대신 KDE(Kernel Density Estimation, 커널밀도추정)를 그려주어 데이터의 분포까지 알 수 있는 발전된 형태의 그래프이다. Boxplot은 데이터의 최대, 최소, 4분위수만 같다면 분포에 상관없이 같은 그래프를 보이지만 violin plot은 분포 또한 확인할 수 있다는 장점이 있다.
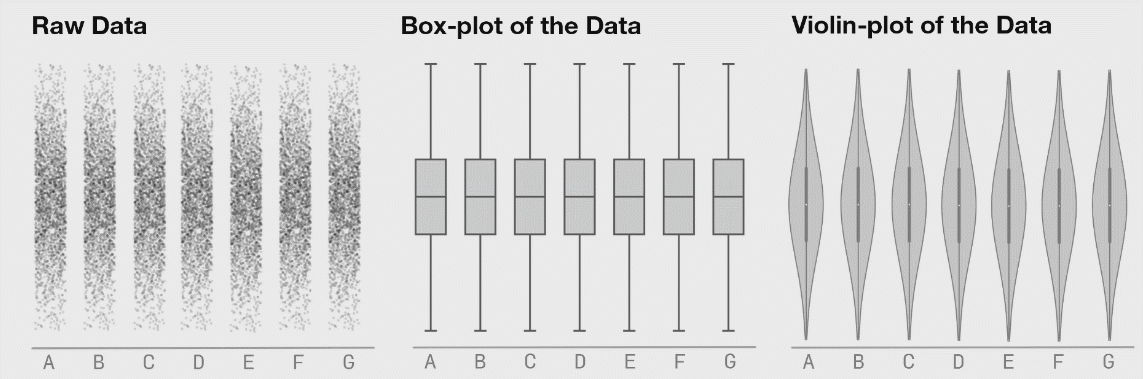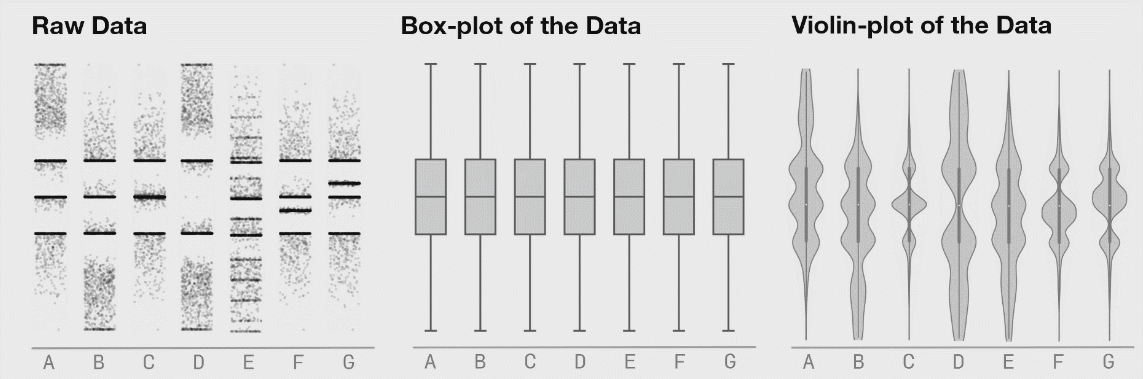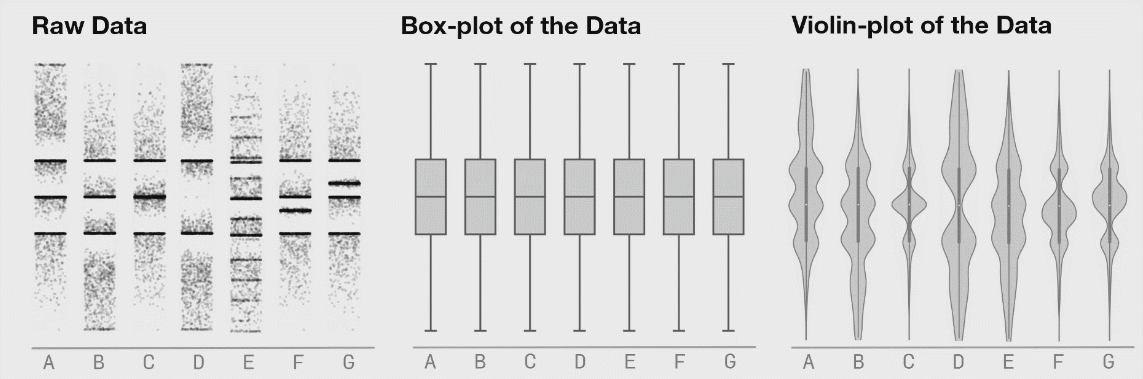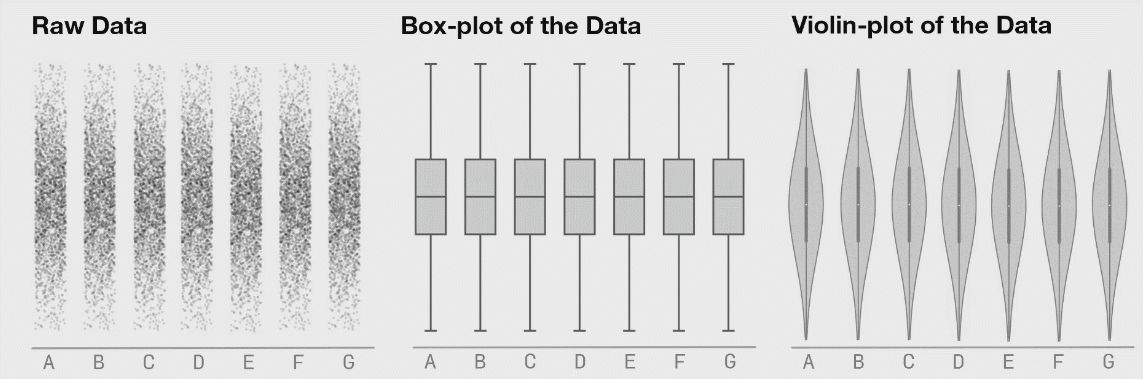(그림 출처 : autodeskresearch)